저는 컴퓨터 과학 전공자가 아닙니다. 워낙 호기심이 많고 몰입하는 성향이라서 어릴 때 애호가로 프로그래밍을 시작했다가 전공을 버리고 프로그래머로 사회생활을 시작한 사람입니다. 그래서 체계적으로 이론 먼저 배우기 보다는 몸으로 먼저 익히고 나중에 이론을 배우면 정리를 하는 편입니다.

재귀 호출도 저에게는 그와 같은 사례 중 하나 입니다. 어릴 때 이런 저런 프로그래밍 관련 지식을 배우면서 알게 되었고 자연스럽게 익혀서 쓰는 기법입니다. 어떤 문제는 재귀가 아니면 쉽게 푸는 방법을 전혀 모르기도 합니다.

시간이 된다면 이 문제를 하나 풀어 보십시오.

미국에는 1 센트, 5 센트, 10 센트, 25 센트 50 센트 등 다섯가지 동전이 있습니다. 이 동전을 무한정 확보할 수 있다고 하면 이들의 조합으로 어떤 금액도 만들 수 있습니다. 특정 금액 m이 주어졌을 때 이 다섯가지 동전을 조합해서 주어진 금액을 만들 수 있는 경우의 수는 몇가지가 있을까요?

꼭 완벽하기 풀지는 않더라도 몇 분 만이라도 어떻게 풀면 될지 생각해 보십시오.

이 문제는 “컴퓨터 프로그램의 구조와 해석”이라는 책의 1.2.2 장에서 “분기되는 재귀”를 설명하는 중에 예제로 나온 유명한 문제입니다. 저는 이 문제를 재귀가 아니면 잘 풀지 못합니다. 제가 재귀로 푼 코드는 다음과 같습니다.

public class ChangeCounter
{
    int cents[] = { 50, 25, 10, 5, 1 };

    public int count(int amount)
    {
        return count(amount, 0);
    }

    private int count(int amount, int idx)
    {
        if (amount == 0)
            return 1;
        else if (amount < 0 || idx >= cents.length)
            return 0;
        else
            return count(amount - cents[idx], idx) + count(amount, idx + 1);
    }
}

어떤 분은 저와는 달리 (스택을 사용한다거나 하는 방법으로) 재귀를 사용하지 않고도 문제를 풀 수 있겠지만 이렇게 단순하게 해결되지는 않을 겁니다. 제가 말하고 싶은 건 재귀는 어떤 문제의 경우 아주 효과적인 해결 방법입니다. 그리고 놀랍게도 별로 어렵지도 않습니다.

저는 최근에 자바 개발자 중에 재귀를 무척 어려운 고급 기법으로 알고 일부러 외면하거나 학습하면서 어려워하는 모습을 보면서 사실 좀 놀랐습니다. 그리고 왜 그러는지 궁금했습니다. 절대 재귀를 어려워하는 분들을 조롱하고 비난한다는 얘기가 아닙니다. 저는 정말 프로그래밍에 숙달된 분 조차 재귀를 어렵게 느끼도록 하는 요인이 뭔지 궁금했습니다. 더 나아가서 그 문제를 풀어 줄 방법도 알고 싶었습니다. 아직 완벽하게 범인을 알아 낸 것은 아니지만 몇몇 용의자를 찾았고 그 중 누가 범인인지 대략 느낌이 갑니다.

무혐의 용의자: 스택 오버 플로 공포증

자바 개발자들과 재귀를 이야기하는 자리에는 늘 스택 오버 플로를 우려하는 목소리가 들립니다. 사실 자바 뿐 아니라 C나 다른 명령형 언어를 사용하는 사람들 가운데에도 이 도시 괴담이 떠도는 것을 보면 역사가 깊은 전설 같습니다. 많은 분들이 프로그래밍에 입문하면서 존경하는 선배나 선임자에게 재귀를 사용하면 스택 오버 플로 오류가 발생해서 프로그램이 멈출 수 있으니 절대! 예외 없이! 언제나! 누구라도! 사용해서는 안된다고 배웠고 이를 금과옥조처럼 여기며 살았던 것입니다.

선배의 말처럼 재귀는 대부분의 언어에서 잘못하면 스택 오버 플로가 발생할 수 있는 위험한 기법입니다. 반복문이 잘못하면 무한 루프에 빠질 수 있는 위험한 기법인 것처럼 말입니다. 사실 프로그래밍을 잘못 작성하지 않는다면 재귀로 인해 스택 오버 플로가 일어나는 일은 흔치 않으며 스택 오버 플로가 발생할 수 있는 상황을 회피하는 방법도 있습니다. 특성을 이해하고 활용하면 도움이 되는 좋은 기법이며 무조건 회피할 이유가 없습니다.

이 공포증이 재귀를 멀리하게 만든 원흉인 것은 맞지만 정작 재귀를 익히면서 어렵다는 생각이 들게 만드는 요인은 아닐 것입니다. 저는 재귀가 어렵지 않다고 생각하고 권했는데 실제로 많은 자바 개발자들이 익히면서 어려워하는 것을 실제로 봤습니다.

첫째 용의자: 높은 난이도

가장 먼저 떠오르는 용의자는 재귀가 정말 이해하기 어려운 기술이라는 주장입니다. 재귀를 별다른 노력 없이 익힌 내가 초천재일지도 모릅니다. IQ 140이 넘는 사람들은 세상 모른 사람들이 자기처럼 머리가 똑똑한 줄 안다고 하더군요.

단언하건데 저는 머리가 그리 좋지 않습니다. 학창 시절에도 성적이 좋지 않았고 사회 생활을 하면서도 늘 제 지능이 평균 수준이라는 사실은 끊임 없이 확인했습니다. 대체로 복잡한 일을 좋아하는 프로그래머 사이에서는 오히려 평균 이하라고 생각됩니다. 따라서 제가 재귀를 별 어려움 없이, 그것도 막 프로그래밍을 배우던 고등학생 시절에 습득했는데 저보다 분명히 똑똑한 많은 사람들이 습득하는 데 곤란을 겪는 이유는 대단히 복잡한 어려운 개념이기 때문이 아닐 겁니다.

둘째 용의자: 분기가 일어나는 반복적 구조 경험 부족

우리가 흔히 경험하는 반복적 구조는 선형적인 반복입니다. 선형적인 반복 상황에서도 재귀를 사용할 수 있고 실제로 함수형 언어에서는 선형 반복에도 재귀를 사용하지만 자바 프로그래머들은 보통 이런 반복 구조는 for나 while 같은 반복문으로 처리합니다. 여러 반복문을 중복하는 2차원, 3차원 등 다차원 반복문도 결국은 선형 반복의 변형일 뿐입니다.

단순한 선형 반복이 아닌, 분기가 일어나는 반복적 상황, 예를 들어 트리 구조 탐색 같은 상황은 일반적인 애플리케이션 프로그래밍, 특히 DB 의존적인 애플리케이션의 개발에는 접할 일이 별로 없습니다. 그런데 이런 형태의 반복적 상황은 선형 반복으로는 해결할 수 없습니다. 반복문과 함께 분기 지점의 상태를 임시로 보관할 스택 같은 자료구조가 별도로 동원되어야 하는데요. 재귀호출을 사용하는 방식과 스택에 할일을 보관하면서 분기를 직접 처리하는 방식은 사실상 동일합니다. 시스템의 호출 스택을 사용할 것이냐 별도의 명시적인 스택을 사용하느냐의 차이 뿐입니다.

선형 반복에도 주로 재귀를 사용하는 함수형 프로그래밍 언어에서는 이미 재귀에 익숙하기 때문에 분기를 처리해야 하는 문제도 큰 어려움 없이 재귀로 해결합니다. 하지만 반복문으로 선형 반복을 처리하던 자바 개발자는 분기 상황에서 갑자기 처리 방법을 재귀로 바꾸거나 스택을 도입해야 하기 때문에 난이도가 갑자기 올라가는 것으로 느낄 것입니다. 그나마 스택을 사용한 번거로운 방법을 조금 더 쉽다고 느끼는 것 같습니다.

이 용의자는 제가 용의자 목록에서 제외 시켰던 첫번째 용의자와 공범일 가능성이 높습니다. 좀 처럼 경험하기 힘들고 복잡한 문제를 해결하는 기술이기 때문에 낯설 뿐 아니라 더 어렵다고 주장할 수 있습니다. 만약 이것이 범인이었다면 전 보다 똑똑한 사람이어야 합니다. 그런데 그다지 똑똑하지 않다고 이미 말씀드렸으므로 성급하게 범인으로 지목하지 않겠습니다.

다만 자바 개발자 입장에서 컬랙션 프레임워크(Collection Framework)가 반복문으로 처리하기 좋게 만들어져있기 때문에 함수형 프로그래밍 언어를 사용하는 사람들과 달리 재귀를 경험할 기회가 별로 없고, 재귀로 풀면 좋은 문제 상황을 드물게 만나면 갑자기 사고하는 방식을 바꿔야 하기 때문에 어렵다고 느낄 수는 있습니다.

셋째 용의자: 제어 흐름 추적 습관

자바는 명령형 프로그래밍 언어입니다. 객체지향 언어를 표방하지만 그 기저에는 명령형 패러다임이 깔려 있습니다. 따라서 우리는 자바로 프로그래밍을 할 때 컴퓨터에게 명령을 내린다고 생각하면서 그 명령의 순서와 분기와 반복을 추적하는 습관을 무의식 중에 훈련합니다.

예를 들어 팩토리얼을 구하는 코드를 작성해 보겠습니다. 팩토리얼은 특정 숫자 n이 주어졌을 때 1부터 n까지의 자연수를 모두 곱한 수이고 n!이라고 표기합니다. 이를 정의하면 다음과 같은 수식으로 표현할 수 있습니다.

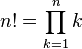
1부터 n까지의 숫자를 모두 곱한 값이므로 이를 코드로 바꾸면 다음과 같이 반복문을 사용해서 계산할 수 있습니다.

int factorial(int n)
{
    int fact = 1;
    for(int c = 1; c <= n; c++)
        fact = fact * c;
    return fact;
}

이 코드를 작성하고 읽을 때 우리는 한줄 한줄 컴퓨터가 실행하는 과정을 단계별로 추적합니다. 결국 우리는 컴퓨터가 어떻게 팩토리얼을 계산하는지 알려준다는 느낌으로 코드를 작성합니다.

팩토리얼을 위와 다른 형태의 식으로 정의할 수 있습니다.

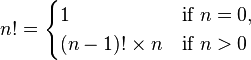
n이 0일 때는 1이고 0보다 클 때에는 (n-1)!와 n의 곱이라는 의미입니다. 이를 코드로 표현하면 다음과 같습니다.

int factorial(int n)
{
    if(n == 0) return 1;
    else return factorial(n-1) * n;
}

보시는 것처럼 위 식을 그대로 코드로 담았습니다. 이 코드는 어떻게 문제를 풀어야 하는지 명령을 내린다는 느낌 보다는 문제 정의 자체를 그대로 코드로 표현한다는 느낌으로 작성했습니다.

핵심은 이렇습니다. 우리가 프로그래밍을 하는 방법은 크게 두 가지입니다. 보통은 우리는 컴퓨터에게 명령을 내려서 문제를 풀게 제어한다는 생각으로 프로그래밍하도록 훈련 받았습니다. 그런데 고수준 언어에서는 이렇게 명령을 내리는 방식 말고 문제 정의를 코드로 표현한다는 느낌으로 코딩하는 방식도 있습니다. 이런 방식을 선언적 프로그래밍이라고 합니다.

결론

저는 확신하는데 재귀를 어렵게 느끼는 이유는 머리가 나빠서도 아니고, 좀 처럼 경험하기 힘든 특수한 상황에서만 필요한 고급 기법이기 때문도 아닙니다.

프로그램을 작성하면서 머리를 굴리는 방식이 다르기 때문입니다. 즉, 어려운 게 아니고 다른 겁니다. 다시 말해 어색한 것이지 난해한 게 아닙니다.

재귀 문제 몇 번 만 풀어보면 금방 감을 잡을 수 있습니다. 물론 명령형으로도 어려운 알고리듬을 만들려면 어려운 것처럼 재귀로도 어려운 알고리듬은 어렵습니다. 하지만 재귀가 어려운 건 아닙니다.

사실 재귀를 쉽게 이해하는 방법까지 이번 글에 담으려고 했는데 오늘은 우리가 재귀를 이해하는 데 어려움을 겪는 이유에 대해서만 적도록 하겠습니다.  다음 기회에 재귀를 설명해 보도록 하겠습니다.

힌트를 드리자면 재귀 코드를 보면 절대 흐름을 추적하려 마십시오. 오히려 문제를 정의한 식으로 보십시오. 그리고 어떤식으로 처리될지 머리에서 CPU를 모의 실험하지 마시고 그 정의가 무엇을 나타내는 정의인지 이해하려고 하십시오.